- Presentations to dance classes at Hope College, Holland, Michigan (1996, 1997).
- Saturday Morning Physics Honors Program presentation at the University of Illinois (2001): as a pdf file (152kB) and as a PowerPoint presentation (871 kB).
- An interesting three-way collaboration with Architecture, Dance, and Physics (2000).
Ken spent four days on campus at the University of Illinois conducting various classes and events relating to the Physics of Dance in September, 2002. Click here for an account of his visit, as well as pictures of some of the events.
Email: g-gollin@uiuc.edu
Phone: (217) 333-4451
Fax: (217) 333-4990
|
5,479 as of February 3, 2002 8,779 as of July 3, 2002 11,162 as of November 14, 2002 13,383 as of January 20, 2003 17,580 as of May 19, 2003 22,847 as of December 20, 2003 28,310 as of May 24, 2004 34,622 as of November 29, 2004 41,267 as of May 17, 2005 56,302 as of March 31, 2006 69,557 as of December 23, 2006 80,640 as of May 20, 2007 103,805 as of May 18, 2008 124,690 as of May 13, 2009 126,646 as of June 7, 2009 |
 |
1. Introduction
8. Jumps (and a comment about black holes)
9. Effects associated with body size
10. What else I'd discuss if I had more
time...
How'd I get myself into this?
- Some statements about dance technique can be restated using a physics vocabulary...
- Interplay between reality (constraints of physical law) and illusion is part of the art...
- Lifts "feel" the way they do for exactly the same reason that a large star will collapse into a black hole...
- Comment about art vs. physics...
Kenneth Laws (a physics professor at Dickinson College) and Cynthia Harvey (previously a dancer with the American Ballet Theater), Physics, Dance, and the Pas de Deux, Schirmer Books, New York, 1994.
Cliff
Frohlich, "The Physics of Somersaulting and Twisting," Scientific
American, pp. 155-164, March, 1980.
Velocity (![]() ):
How fast and in what direction something is moving.
):
How fast and in what direction something is moving.
Momentum (![]() ):
The magnitude of an object's momentum gives an indication of how hard it
is to bring it to a stop.
):
The magnitude of an object's momentum gives an indication of how hard it
is to bring it to a stop.
momentum = mass x velocity (![]() )
)
(Heavy but slow, light but fast... both are hard to stop.)
Force (![]() ):
Just like you'd think. It's a push, characterized by a magnitude (how hard)
and a direction.
):
Just like you'd think. It's a push, characterized by a magnitude (how hard)
and a direction.
Force changes momentum:
- The harder you push, the more rapidly the momentum changes.
- The longer you push, the greater the total change in momentum.
-
The equation:
 .
.
If you don't push on something its direction of travel
doesn't change. Note that ![]() point in the same direction.
point in the same direction.
If you do push on something, you can change its speed
and/or its direction of travel.
Cart on air track feels two forces:
- gravity
- up & slightly to-the-left push from air track (there's no frictional force parallel to the air track)

The net force causes the change in the cart's momentum.
Net force on a dancer: gravity (down) + support from floor
(up) + friction from floor (sideways)
Angular velocity (![]() ):
How fast something spins and in what direction its rotation axis
points.
):
How fast something spins and in what direction its rotation axis
points.

Angular momentum (![]() ):
The magnitude of an object's angular momentum gives an indication of how
hard it is to bring it to a stop.
):
The magnitude of an object's angular momentum gives an indication of how
hard it is to bring it to a stop.
angular momentum = rotational inertia x angular velocity.
(![]() )
)
(Large rotational inertia, but spinning slowly; small rotational inertia but spinning rapidly... both are hard to stop.)
Centrifugal force: Effective force pushing something to the outside of a turn.
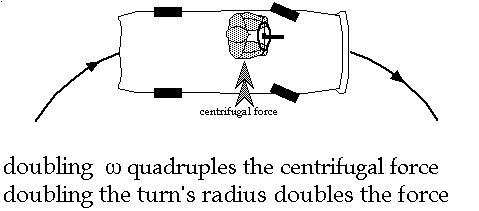
Torque (![]() ):
"Off center" force(s) which can cause something to spin.
):
"Off center" force(s) which can cause something to spin.

Torque changes angular momentum:
- The harder you push, the more quickly the object "spins up."
- The further from the spin axis you apply the forces used to generate the torque, the more quickly the object "spins up."
- The longer you push, the greater the total change in angular momentum.
-
The equation:
 .
.
If no torque is applied to a rigid object, its spin axis doesn't wobble.
Objects which change shape (dancers!!) are more complicated:
their rotational inertia (![]() )
changes with time (more on this later...)
)
changes with time (more on this later...)
We all know what it means.... In physics terms:
- Net force is zero (otherwise your momentum would change: you might fall)
- Net torque is zero (otherwise your angular momentum would change: you might tip over)

Reason for the name: net effect of gravity on an object (a dancer) is the same as if it were only acting at the c.g., and not on all parts of the object.
Forces on a balanced dancer: gravity (pulls down, acts at c.g.) + support from floor (pushes up, acts at feet)
Keith Roberts (ABT) in The Rite of Spring, photo by Roy Round
Forces sum to zero.
Both forces "point through" the dancer's center of gravity, so torque is zero.
More complicated example:
Sandra Brown and Johann Renvall (ABT) in Airs, photo by Nancy Ellison
Forces on each dancer sum to zero.
Though some forces are "off-center", the torques also sum to zero.
Obviously, the net torque (and force) won't be zero if only one dancer is present:

Staying balanced: dancer's center of gravity must remain directly above the area of contact with the floor. (Otherwise,

Smaller floor contact area (en pointe, for example)
makes balance more difficult.
Maintaining balance:
- shift foot to move floor contact area
- adjust arms/legs/torso to move c.g.
Two distinct "physics domains" here:
- slow turns: maintain static balance
- fast turns: rotation axis shouldn't wobble (much)

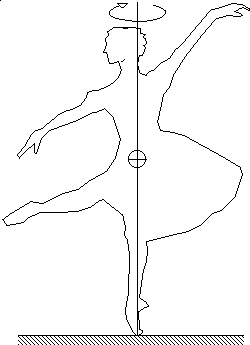
Not all positions which are statically balanced can be held in a turn.
An example:
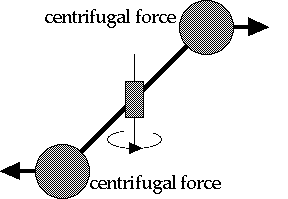

Centrifugal forces exert a torque, throwing the dancer off balance. Shift center of gravity to maintain dynamic (but not static) balance

Reminders:
-
 stands for angular momentum
stands for angular momentum -
 stands for rotational inertia
stands for rotational inertia -
 stands for angular velocity
stands for angular velocity -
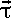 stands for torque
stands for torque -
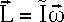
-

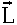 is constant.
is constant.
-
Decrease
 :
:  must increase (spin faster).
must increase (spin faster). -
Increase
 :
:  must decrease (spin slower).
must decrease (spin slower).
 is a measure of how difficult it
is to start something spinning. (Just as mass is an indication of how difficult
it is to start something moving.)
is a measure of how difficult it
is to start something spinning. (Just as mass is an indication of how difficult
it is to start something moving.)
Calculating
 :
:
-
greater mass -> larger
 (doubling
the mass doubles
(doubling
the mass doubles  )
) -
mass distributed farther from rotation axis -> larger
 (doubling
the distance quadruples
(doubling
the distance quadruples  )
) -
 (one mass)
(one mass) -
 (several masses)
(several masses)
Increasing
 decreases the
spin rate.
decreases the
spin rate.  quadruples in the figure:
quadruples in the figure:

Because of "conservation of angular momentum," you can change the speed of a turn when en pointe by extending or retracting a leg.
No torque is involved!

Friction between the floor and your foot (or feet) can also generate a torque. Swinging a leg going into a turn works like this:

You push on the floor one way, the floor pushes back the other way. (You can't do this on a slippery floor!)
Turns in the air: no forces except gravity can act on the dancer.
Angular momentum stays constant: changing  (by changing the orientation of arms, legs,...) will change
(by changing the orientation of arms, legs,...) will change ![]() correspondingly.
correspondingly.
Ever see a falling cat right itself? The cat has zero angular momentum at all times, but somehow manages to turn over.
It works like this:
- Upside-down cat curves its back "the easy way."
- Cat straightens its back while bending around its middle to its right.
- Cat comes out of its bend-to-the-right while arching its back "the hard way."
- Cat straightens its back while bending around its middle to its left.
- Cat comes out of its bend-to-the-left while curving its back "the easy way."
Here's a diagram:
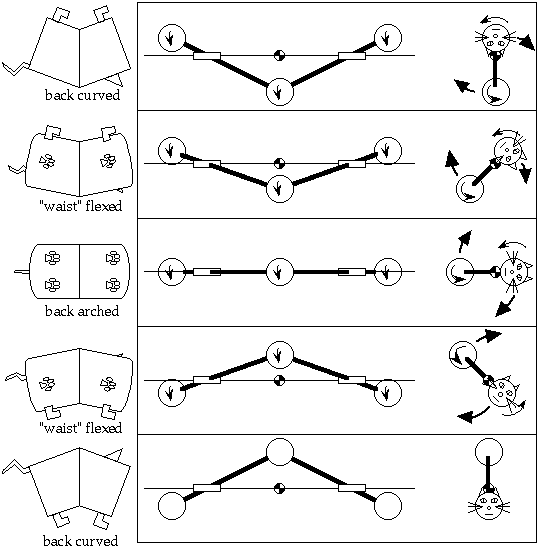
Dancers can also perform zero-angular-momentum turns. Some are catlike, some not...
In some moves, the body parts which carry the initial angular momentum change during the course of the turn. An example: a tour jeté. The angular momentum associated with the raising of the left leg (1) is taken up by the trunk and arms (2), then the left leg (3), then both legs (4).

The diagram is based on photos in Laws' and Harvey's book.
Gravitational force depends on mass:
- more massive -> greater gravitational pull
- mass is to gravity like electric charge is to electrostatics: in electrostatics: the larger the electric charge something has, the greater the force it feels in an electric field.
This is very curious. Why should an object's momentum/velocity relationship have anything at all to do with the gravitational pull on that object? (Doubling an object's mass both doubles its momentum and doubles the strength of the gravitational force it experiences.)
The equivalence of "gravitational" and "inertial" mass gives rise to Einstein's General Theory of Relativity. Black holes, curved spacetime, and so on!
Gravity is the only force acting on a dancer in mid-air.
Recall: net effect of gravity is the same as if it were only acting at the dancer's center of gravity.
Gravitational force:
![]()
(![]() is a constant)
is a constant)
Connection between force and momentum:
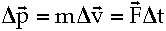
Grav. acceleration is independent of mass:
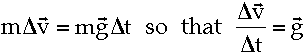
Anything you drop speeds up at the same rate; anything thrown straight up slows at the same rate. (Vertical) speed changes by 32 feet per second (about 22 miles per hour) for each second in the air.
If you could jump so that your initial vertical velocity was 32 ft/sec, your center of gravity would travel up for 1 second, pause for an instant, then spend the next second falling.
If you could only jump with an initial velocity of 16 ft/sec, your c.g. would travel up for 1/2 second, pause, then fall for the next 1/2 second.
Note the following: in the 16 ft/sec case, you'd ascend for half as long, and leave the ground going half as fast as in the 32 ft/sec case. Net effect: you'd only jump one-fourth as high.
The equations:
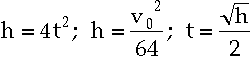
- t is duration of jump (in seconds)
-
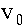 is initial vertical velocity
is initial vertical velocity - h is height, measured in feet.
Jumping in time to music:
-
Since
 ,
half-second duration jumps must raise the dancer's c. g. by one
foot
,
half-second duration jumps must raise the dancer's c. g. by one
foot - Height of the dancer will influence how this looks: a six-foot-tall dancer jumps 1/6 of his height, a five-foot-tall dancer jumps 1/5 of her height.
- a six-foot dancer executing a 1/5-his-height jump will stay in the air for about 0.55 seconds, instead of 0.50 seconds (he can only do 9 jumps in 5 seconds, instead of 10)
| height of jump | time in the air | initial velocity |
| 6 inches | 0.35 seconds | 5.66 feet/sec |
| 1 foot | 0.50 seconds | 8.00 feet/sec |
| 1 foot 6 inches | 0.61 seconds | 9.80 feet/sec |
| 2 feet | 0.71 seconds | 11.31 feet/sec |
Position of a dancer's center of gravity vs. time during a jump:
- Gravity only influences the vertical component of motion, not the horizontal:
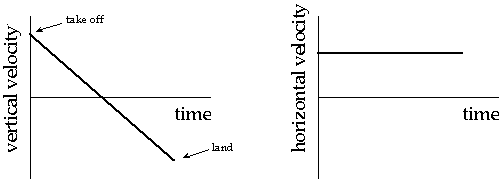
- Height vs. time is a parabola, while horizontal distance vs. time is a straight line:
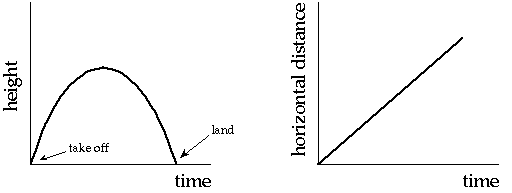
The dancer's trajectory in a jump is also a parabola. For a 2 foot rise in the height of the dancer's center of gravity, and a 10 ft/sec horizontal velocity, the path will look like this:

By raising his/her legs (changing the distance between the center of gravity and his/her head)...

The dancer can create an illusion of floating:

The vertical motion of the head is smaller than the motion of the center of gravity.
In addition, half the duration of the jump is spent between
the points indicated by the arrows; the height of the dancer's center of
gravity only changes by 6 inches during this time.
There are lots of them. A simple model: all dancers are "shaped the same," but come in different heights.
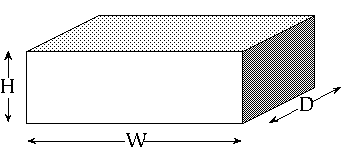
Recall that volume is H x W x D. Increasing the length of each side by 10% will increase the volume by a factor of 1.1 x 1.1 x 1.1 or 1.33 (a 33% increase).
Rotational inertia is proportional to mass x the square of the distance from the rotation axis to the outer surface of an object. Increasing the linear dimensions of a dancer by 10% will increase the rotational inertia by a factor of 1.1 to the fifth power, or 1.61 (a 61% increase).
Here is a table describing the scaling of a number of quantities with a 10% increase in a dancer's height:
| quantity |
|
|
| height |
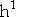 |
|
| weight |
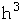 |
|
| rotational inertia of entire body |
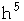 |
|
| rotational inertia of leg about hip |
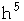 |
|
| energy to jump 1 ft |
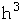 |
|
| energy to jump to 30% of own height |
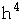 |
|
| energy to swing leg 90 deg. in 1 sec. |
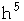 |
|
| duration of a 30%-of-height jump |
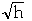 |
|
- dancing with a partner
- effects relating to body size in more detail
- impact and stress injuries.
To Erica Wilson-Perkins, Linda Lehovec, and Renée Wadleigh at the University of Illinois: thank you for allowing me to watch your classes in jazz, ballet, and modern dance techniques.
To Rebecca Nettl-Fiol and Sean Sullivan, also of the University of Ilinois, and for Linda Graham of Hope College: thank you for your interest and time spent discussing dance with me.